33: Komal Jogdand,  34: Ameya Joshi,  35: Ranbeer Kadam,  36: Sonal Kadam,  37: Viraj Kadlag

Guide: Prof. Nitin Borse

 BOUNDARY LAYER

Fig. 1: Laminar and Turbulent Flow

Introduction:

When a real fluid is flowing through a solid object, the particles of fluid tend to adhere to the boundary. This gives rise to no slip condition. This means that the velocity of fluid near the boundary would be same as boundary of object. If the object is stationary then the velocity of fluid flowing near the boundary has zero velocity. As we go further from the boundary condition the velocity of fluid increases which results in variation of velocity which give rise to velocity gradient. Let’s assume the velocity of free stream is U in direction of normal to boundary. This variation of velocity occurs in narrow region near to solid boundary. This narrow region is called the boundary layer. The theory dealing with the study of the boundary layer is called boundary layer theory.

According to the theory, there are two regions that can be distinguished regarding flow of fluid near the solid boundary.

1.      A very thin layer called the boundary layer, which is in the immediate neighborhood of the solid boundary where the variation of velocity from zero to U takes place in a direction normal to solid boundary. In this region, velocity gradient exists and fluid exerts shear stress on the object in direction of motion of the fluid.

The value of shear stress can be expressed as 

                                                                   

2.     The other part is the remaining fluid, which is outside the boundary layer. There the velocity is constant and equal to U. As there is no variation in velocity, velocity gradient does not exist in this region. As a result, the shear stress is zero.

Laminar Boundary Flow:

Consider the flow of fluid, having free stream velocity as U, over a flat plate which is placed parallel in direction of the flow of fluid. Let us consider the plate is stationary.

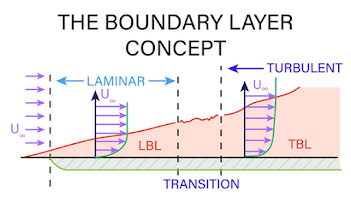Fig. 2: Boundary Layer Concept

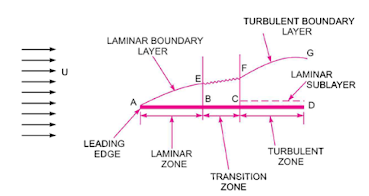Fig. 3

As plate is stationary, velocity of fluid near the surface of object is zero. But as we go further from surface, there is certain velocity of fluid. The fluid with uniform velocity U is retarded in the vicinity of the solid surface of the plate and boundary layer region begins at the sharp leading edge. Near the leading edge of the surface of plate where the thickness is small, the flow of boundary layer is laminar though the main flow is turbulent. This layer of the fluid is said to be laminar boundary layer (AE). The length of plate from the leading edge, up to which laminar boundary layer exists, is called laminar zone. AB shown is laminar zone. The distance of B is obtained from Reynold number which is equal to 5*10⁵ for plate. Because up to Reynolds number flow is laminar.

x: Distance from leading edge

U: Free stream velocity

v: Kinematic viscosity

If we know values of U and viscosity of fluid, we can find the range of laminar flow.

Turbulent Boundary Layer:

As we go further from laminar zone, the thickness of boundary layer will go on increasing in downstream direction. Here the motion of fluid is disturbed and unstable which leads transition from laminar to turbulent boundary layer. This is called transition zone (BC). The further downstream the layer grows thicker which is called turbulent boundary layer (FG).

Laminar Sub-Layer:

This region is in turbulent boundary layer zone, adjacent to solid surface of the plate. In this region, the velocity variation is caused due to viscous force. Velocity variation is linear and velocity gradient is constant.

     Thus, the shear stress in the sub layer is 

Boundary Layer Thickness (δ):

Defined as distance from the boundary of object in y- direction to the point, where the velocity of fluid is approximately 0.99 times U.

Displacement Thickness (δ*):

Defines as distance measured perpendicular to the boundary of object, by which the boundary should be displaced to compensate for the reduction in flow rate on account of boundary layer formation

                                               

Momentum Thickness (θ):

Defined as distance measured perpendicular to the boundary, by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation.

Energy Thickness (δ**):

Defined as the distance measured perpendicular to the boundary of the object, by which the boundary should be displaced to compensate for the reduction in kinetic energy of the flowing fluid on account of boundary layer formation.

     Drag Force on the flat plate due to boundary layer:

The drag force on the plate can be determined if the velocity profile near the plate is known.

Fig. 4: Drag Force on Plate

 

: Shear Stress

: Density of Fluid

       U      : Velocity of free stream

This equation is known as Von Karman momentum integral equation for boundary layer formation

This is applied to laminar, turbulent and transition layers flows.

Total Drag on plate of length L is:

Local Co-efficient of Drag:

Defined as ratio of shear stress to half of density and square of velocity of  free stream.

Average Co-efficient of Drag:

Defined as ratio of the total drag force to half of density, area and square of velocity of  free stream. It is called coeffient of drag.

Boundary Condition for Velocity Profile:

Following conditions should be satisfied, whether it is laminar or turbulent flow:

SEPARATION OF BOUNDARY LAYER

When a solid body is immersed in a flowing fluid, a thin layer of fluid called the boundary layer is formed adjacent to the solid body. In this thin layer of fluid, the velocity varies from zero to free-stream velocity in the direction normal to the solid body. Along the length of the solid body, the thickness of the boundary layer increases. The fluid layer adjacent to the solid surface has to do work against surface friction at the expense of its kinetic energy. This loss of kinetic energy is recovered from the immediate fluid layer in contact with the layer adjacent to the solid surface through the momentum exchange process. Thus the velocity of the layer goes on decreasing. Along the length of the solid body, at a certain point, a stage may come when the boundary layer may not be able to keep sticking to the solid body if it cannot provide kinetic energy to overcome the resistance offered by the solid body. In other words, the boundary layer will be separated from the surface. This phenomenon is called the boundary layer separation. The point on the body at which the boundary layer is on the verge of separation from the surface is called the point of separation.

References:

1. http://www.musaliarcollege.com/e-Books/ME/Fluid%20Mechanics%20&%20Hydraulic%20Machines.pdf
2. https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3Dk37vPSA3E1g&psig=AOvVaw1
3. https://aerospaceengineeringblog.com/boundary-layers/